THE METHOD OF LEAST SQUARES REVEALED
GAUSS, CARL FRIEDRICH
Theoria motus corporum coelestium in sectionibus conicis solem ambientium.
Hamburg, Frid. Perthes & I.H. Besser, 1809.
4to (224 x 261 mm). In a later full cloth binding with gilt lettering to spine and blindtooled borders to boards. Very few occassional brownspots. A fine and clean copy. [Blank], XI, (1), 227, (1), 20, [blank] pp. + 1 folded plate.
First edition of this epochmaking work in mathematical statistics and mathematical and computational astronomy. Here, Gauss revealed for the first time his method of least squares which became “the dominant theme – the leitmotif – of nineteenth-century mathematical statistics” (Stigler, p. 11). Together with his ‘Disquisitiones Arithmeticae’ this work “established his reputation as a mathematical and scientific genius of the first order.” (DSB) Here he presented “an analysis of the problems arising in the determination of the motions of the planets and comets from a limited number of observational data" (PMM 257 note). "In this work Gauss systematically developed the method of orbit calculation from three observations he had devised in 1801 to locate the planetoid Ceres, the earliest discovered of the 'asteroids,' which had been spotted and lost by G. Piazzi in January 1801." (Norman 879). Sparrow 81.
On January 1, 1801, the Italian astronomer Giuseppe Piazzi discovered the planetoid Ceres, but could only observe it for few days before it was lost in the glare of the Sun until the end of the year. After so many months of not being observed it was not possible to calculate with existing methods at which position it should reappear. Gauss, however, at an age of 24, astounded the world, when in December of that same year he predicted the exact location at which Ceres could again be observed. He did not reveal how he had calculated the orbit of Ceres. Only in 1809, when Gauss published his second book "Theoria motus corporum coelestium in sectionibus conicis solem ambientium" (the offered item), did he reveal his new method of orbit calculation.
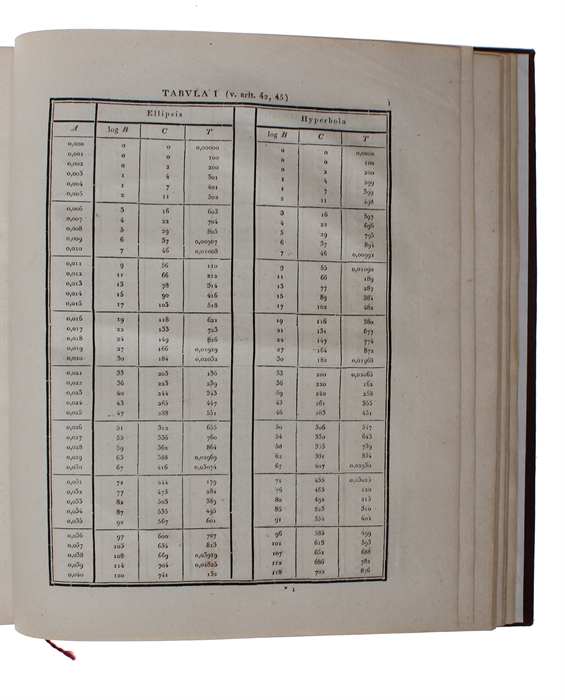
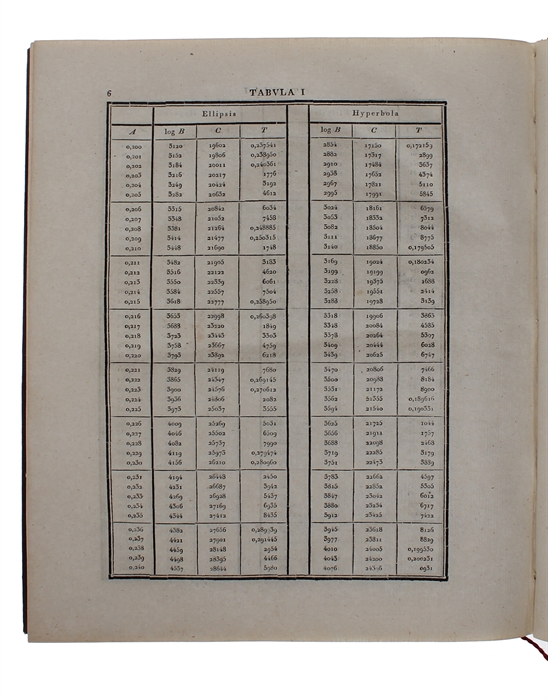
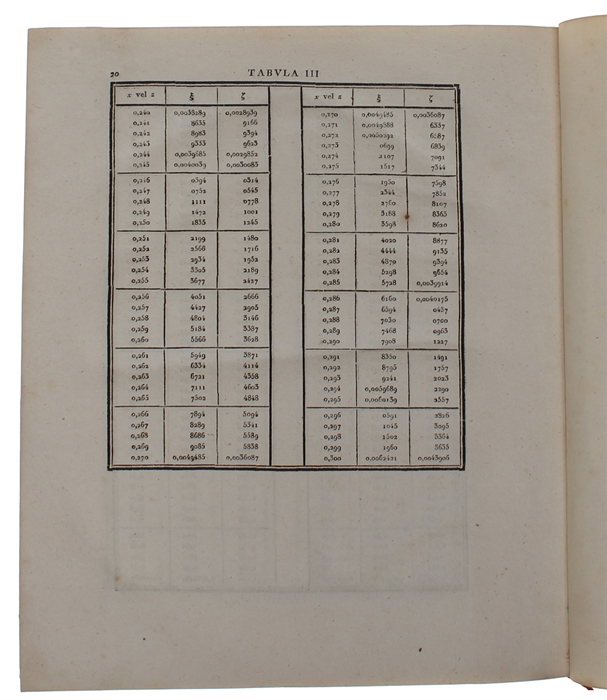
In the first part he dealt with differential equations, conic sections and elliptic orbits, while in the second part, the main part of the work, he showed how to estimate and then to refine the estimation of a planet's orbit using a new method involving minimizing the sum of squared residuals, i.e. the method of least squares. He was able to prove the correctness of the method under the assumption of normally distributed errors. It is here that the Gaussian curve, expressing statistical distribution in probability, makes its first appearance.
Barchas 792.
Norman 879.
Dibner 114n.
PMM 257 (Mentioned in note).
Hald: History of Mathematical Statistics 1750-1930, pp.351-357.
Order-nr.: 60237